双线性内插法
#数字图像处理
我将最近学数字图像处理,写的一些代码放到了github 中保存,有机会一起学习。有错误和需要补充的地方欢迎评论。
理论简介
双线性插值是图像内插缩放的一种方法。
简单来说,双线性插值即对于目标像素进行两个方向上的线性插值。
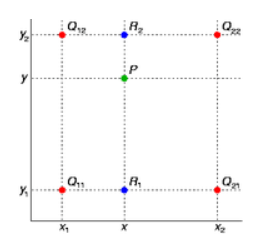
比如,首先在x上进行一次线性插值得到两个点,即上图得到的
R
1
R_1
R1,
R
2
R_2
R2。再在y方向上进行一次线性插值,由
R
1
R_1
R1,
R
2
R_2
R2 得到目标点
P
P
P。
故双线性插值需要四个最近邻像素点(原像素点,即已知灰度值),即上图中的 Q 11 , Q 12 , Q 21 , Q 22 Q_{11},Q_{12},Q_{21},Q_{22} Q11,Q12,Q21,Q22。
与最近邻内插法相比较
同样是上图,若求转换后的目标点 P P P 的灰度值,我们只需要在原图像中找最接近的像素,将其值赋给 P P P即可,上图的话即将 Q 12 Q_{12} Q12 赋值给 P P P。
引用《数字图像处理-第三版-冈萨雷斯》书上:
假设一副大小为 500x500 的像素的图像要放大 1.5 倍到 750x750 像素。一种简单的放大方法是创建一个假象的 750x750 网格, 它与原始图像有相同的间隔,然和将其收缩,使它准确地与原图像匹配。显然,收缩后的 750x750 网格的像素间隔要小于原图像的像素间隔。
为了对覆盖的每一个点赋以灰度值,我们再原图像中寻找最接近的像素,并把该像素的灰度赋给 750x750 网格中的新像素。
这里不对最近邻内插法做详细讨论。但在这里引出冈萨雷斯这本书上这段话是为了方便理解这种“网格”的思想。故: 上图中, Q 11 , Q 12 , Q 21 , Q 22 Q_{11},Q_{12},Q_{21},Q_{22} Q11,Q12,Q21,Q22 即原图像上相邻的 2x2 的4个像素点,对于缩放后的新的图像上的一个像素点,它也会在如上图 P P P点 那般位于一个网格之中。
因此能找到四个最近邻点,再借助这四个点即可进行双线性内插法。
线性插值公式
如第一段所说,双线性内插即进行了两次线性插值,所有我们需要先知道线性插值。以下图为例:
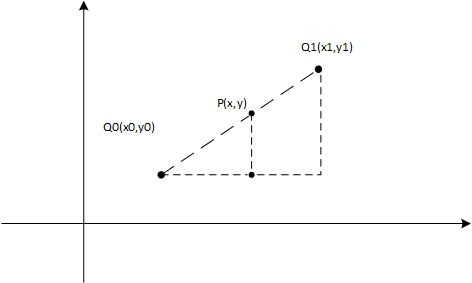
因为
y
−
y
0
x
−
x
0
=
y
1
−
y
0
x
1
−
x
0
\frac{y-y_0}{x-x_0} = \frac{y_1 - y_0}{x_1-x_0}
x−x0y−y0=x1−x0y1−y0
所以可以得出
y
=
x
1
−
x
x
1
−
x
0
y
0
+
x
−
x
0
x
1
−
x
0
y
1
y = \frac{x_1 - x}{x_1 - x_0}y_0 + \frac{x - x_0}{x_1 - x_0}y_1
y=x1−x0x1−xy0+x1−x0x−x0y1
所以双线性即在两个方向上都进行一次线性插值即可,只是在第一个由四个点 Q 11 , Q 12 , Q 21 , Q 22 Q_{11},Q_{12},Q_{21},Q_{22} Q11,Q12,Q21,Q22 上计算两个点,第二次由两个点线性插值算出目标点即可。
双线性插值公式

还是这个图(此图来源于网络),
Q
11
,
Q
12
,
Q
21
,
Q
22
Q_{11},Q_{12},Q_{21},Q_{22}
Q11,Q12,Q21,Q22为近邻点,
P
P
P 为待求点。
设算子
f
(
⋅
)
f(\cdot)
f(⋅) 代表该像素原图像的灰度值。
Q
i
j
Q_{ij}
Qij的坐标为:
(
x
i
,
y
j
)
(x_i,y_j)
(xi,yj)
则第一次线性插值计算
R
1
R_1
R1、
R
2
R_2
R2:
(也用
R
1
R_1
R1、
R
2
R_2
R2分布代表他们的线性插值得到的灰度值)
R
1
=
x
2
−
x
x
2
−
x
1
f
(
Q
11
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
21
)
R
2
=
x
2
−
x
x
2
−
x
1
f
(
Q
12
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
22
)
R_1 = \frac{x2 -x}{x2-x1}f(Q_{11}) + \frac{x-x_1}{x_2-x_1}f(Q_{21}) \\ R_2 = \frac{x2 -x}{x2-x1}f(Q_{12}) + \frac{x-x_1}{x_2-x_1}f(Q_{22}) \\
R1=x2−x1x2−xf(Q11)+x2−x1x−x1f(Q21)R2=x2−x1x2−xf(Q12)+x2−x1x−x1f(Q22)
第二次插值:
P
=
y
2
−
y
y
2
−
y
1
R
1
+
y
−
y
1
y
2
−
y
1
R
2
P = \frac{y2-y}{y2-y1}R_1 + \frac{y-y1}{y2-y1}R_2
P=y2−y1y2−yR1+y2−y1y−y1R2
还记得提到过: Q 11 , Q 12 , Q 21 , Q 22 Q_{11},Q_{12},Q_{21},Q_{22} Q11,Q12,Q21,Q22为近邻点吗,所以上面各式的分母 y 2 − y 1 , x 2 − x 1 y_2 -y_1,x_2-x_1 y2−y1,x2−x1都等于 1 1 1。
于是最终得到:
P
=
f
(
Q
11
)
(
x
2
−
x
)
(
y
2
−
y
)
+
f
(
Q
21
)
(
x
−
x
1
)
(
y
2
−
y
)
+
f
(
Q
12
)
(
x
2
−
x
)
(
y
−
y
1
)
+
f
(
Q
22
)
(
x
−
x
1
)
(
y
−
y
1
)
P = f(Q_{11})(x_2-x)(y_2-y) + \\ f(Q_{21})(x-x_1)(y_2-y)+\\ f(Q_{12})(x_2-x)(y-y_1)+\\ f(Q_{22})(x-x_1)(y-y_1)
P=f(Q11)(x2−x)(y2−y)+f(Q21)(x−x1)(y2−y)+f(Q12)(x2−x)(y−y1)+f(Q22)(x−x1)(y−y1)
Tips
源图像和目标图像几何中心的对齐
方法:在计算源图像的虚拟浮点坐标的时候,
一般情况左上角对齐:
s
r
c
X
=
d
s
t
X
∗
(
s
r
c
W
i
d
t
h
/
d
s
t
W
i
d
t
h
)
srcX=dstX * (srcWidth/dstWidth)
srcX=dstX∗(srcWidth/dstWidth) ,
s
r
c
Y
=
d
s
t
Y
∗
(
s
r
c
H
e
i
g
h
t
/
d
s
t
H
e
i
g
h
t
)
srcY = dstY * (srcHeight/dstHeight)
srcY=dstY∗(srcHeight/dstHeight)
中心对齐:
S
r
c
X
=
(
d
s
t
X
+
0.5
)
∗
(
s
r
c
W
i
d
t
h
/
d
s
t
W
i
d
t
h
)
−
0.5
SrcX=(dstX+0.5)* (srcWidth/dstWidth) -0.5
SrcX=(dstX+0.5)∗(srcWidth/dstWidth)−0.5
S
r
c
Y
=
(
d
s
t
Y
+
0.5
)
∗
(
s
r
c
H
e
i
g
h
t
/
d
s
t
H
e
i
g
h
t
)
−
0.5
SrcY=(dstY+0.5) * (srcHeight/dstHeight)-0.5
SrcY=(dstY+0.5)∗(srcHeight/dstHeight)−0.5
我在代码中都有实现,但目前没有看出有明显的效果,可能需要用更大的图片试试。(通过在类初始化中定义参数 align = 'left', 该参数默认为 center)
过程中遇到的问题
按照中心对其的思路写的时候,发现在 1、3、5、7倍缩放的时候,会发生意外。体现在 1倍缩放得到一个全黑的图像,缩放失败。3倍缩放时得到一个相比于原图较暗的图像,5倍缩放得到一个相比于原图较暗但比3倍时亮的图像,7倍时同理。
经过查看 src_i 等数值变换,发现在中心对齐法中 ,可能会出现 src_i (即上面公式中的
S
r
c
X
、
S
r
c
Y
SrcX、SrcY
SrcX、SrcY)值为一个整数的情况,使其在向上取整和向下取整得到一个相同的值。
例如对 235x233 的图像,经过三倍缩放,在
d
s
t
i
=
115
dst_i = 115
dsti=115 时,经过中心对齐的公式,计算出的
s
r
c
i
=
38
src_i = 38
srci=38
(
115
+
0.5
)
∗
235
235
∗
3
−
0.5
=
38
(115+0.5)* \frac{235}{235*3} -0.5 = 38
(115+0.5)∗235∗3235−0.5=38
为解决这个问题,我使计算出的 src_i += 0.001 ,再进行向上和向下取整。 OK,虽然比较偷懒加取巧,但确实解决了这个问题。
ps: 更合理的解决方案,应该是对于得到的整数坐标,直接将对应的原像素坐标赋值给新点即可,即对于这种点不采用双线性变换,直接恒等映射,这样保证了信息不丢失。 这里先插个旗,之后再看我有时间改没。
python_91">基于 numpy 的python代码实现
纯手打,实测可用。
python"># 引入必要的包
import numpy as np
import matplotlib.image as mpimg # 用于读取
import matplotlib.pyplot as plt # 用于显示
import logging
from math import ceil
# 双线性插值法
class BilinearInterpolation(object):
def __init__(self,
w_rate: float, # w 的缩放率
h_rate: float, # h 的缩放率
*,
align='center'
):
if align not in ['center', 'left']:
logging.exception(f'{align} is not a valid align parameter')
align = 'center'
self.align = align
self.w_rate = w_rate
self.h_rate = h_rate
pass
def set_rate(self,
w_rate: float, # w 的缩放率
h_rate: float # h 的缩放率
):
self.w_rate = w_rate
self.h_rate = h_rate
# 由变换后的像素坐标得到原图像的坐标 针对高
def get_src_h(self, dst_i,source_h,goal_h) -> float:
if self.align == 'left':
# 左上角对齐
src_i = float(dst_i * (source_h/goal_h))
elif self.align == 'center':
# 将两个图像的几何中心重合。
src_i = float((dst_i + 0.5) * (source_h/goal_h) - 0.5)
src_i += 0.001
src_i = max(0.0, src_i)
src_i = min(float(source_h - 1), src_i)
return src_i
pass
# 由变换后的像素坐标得到原图像的坐标 针对宽
def get_src_w(self, dst_j,source_w,goal_w) -> float:
if self.align == 'left':
# 左上角对齐
src_j = float(dst_j * (source_w/goal_w))
elif self.align == 'center':
# 将两个图像的几何中心重合。
src_j = float((dst_j + 0.5) * (source_w/goal_w) - 0.5)
src_j += 0.001
src_j = max(0.0, src_j)
src_j = min((source_w - 1), src_j)
return src_j
pass
def transform(self, img):
source_h, source_w, source_c = img.shape # (235, 234, 3)
goal_h, goal_w = round(
source_h * self.h_rate), round(source_w * self.w_rate)
new_img = np.zeros((goal_h, goal_w, source_c), dtype=np.uint8)
# print the goal image's shape
# print(new_img.shape[0], new_img.shape[1])
# i --> h , j --> w
# x --> w:j y --> h:i
for i in range(new_img.shape[0]): # h
src_i = self.get_src_h(i,source_h,goal_h)
for j in range(new_img.shape[1]):
src_j = self.get_src_w(j,source_w,goal_w)
i2 = ceil(src_i)
i1 = int(src_i)
j2 = ceil(src_j)
j1 = int(src_j)
# i 对应 y , j 对应 x
# x 对应 j , y 对应 i
x2_x = j2 - src_j
x_x1 = src_j - j1
y2_y = i2 - src_i
y_y1 = src_i - i1
# print(i,j,src_i,i1,i2,src_j,j1,j2)
# f(Q_xy) 对应 img[y,x] 即 img[i,j]
new_img[i, j] = img[i1, j1]*x2_x*y2_y + img[i1, j2] * \
x_x1*y2_y + img[i2, j1]*x2_x*y_y1 + img[i2, j2]*x_x1*y_y1
return new_img
pass
pass
# 读取图片并显示
pic1 = mpimg.imread('./hw1_picture1.jpg')
pic2 = mpimg.imread('./hw1_picture2.jpg')
pic3 = mpimg.imread('./hw1_picture3.jpg')
print(pic1.shape)
# Show original image --- hw1_picture1.jpg
plt.imshow(pic1)
plt.axis('off')
plt.show()
# 0.5 缩放
BI = BilinearInterpolation(0.5,0.5)
new_pic1_half = BI.transform(pic1)
plt.imshow(new_pic1_half)
plt.axis('off')
plt.show()
new_pic1_half = BI.transform(pic2)
plt.imshow(new_pic1_half)
plt.axis('off')
plt.show()
new_pic1_half = BI.transform(pic3)
plt.imshow(new_pic1_half)
plt.axis('off')
plt.show()
#3倍缩放
BI = BilinearInterpolation(3,3)
new_pic = BI.transform(pic1)
plt.imshow(new_pic)
plt.axis('off')
plt.show()
new_pic = BI.transform(pic2)
plt.imshow(new_pic)
plt.axis('off')
plt.show()
new_pic = BI.transform(pic3)
plt.imshow(new_pic)
plt.axis('off')
plt.show()
代码的运行速度较慢,看了下其他大牛给出的优化方法以及opencv的优化方法,由于时间关系没有深入探究,这里先mark住,之后需要的时候再详细探究。
以下图片来自深入理解双线性插值算法_Activewaste-程序员秘密 - 程序员秘密

end
记录学习,关于代码和理论,若有错误欢迎指正、补充!♥
参考:
- 最近邻插值和双线性插值原理 - 知乎
- 深入理解双线性插值算法_Activewaste-程序员秘密 - 程序员秘密